Podle autora článku [X1] je souhra mezi teorií superstrun (superstring theory) [F1] a moderní kosmologií velmi slibná. Až se teorie superstrun stane kvantovou teorií prostoročasu a sjednotí všechny silové interakce přírody, zřejmě také vyřeší většinu koncepčních problémů dnešních kosmologických modelů vesmíru v jeho počátečních fázích vývoje.

Kosmologie počátečních fází vývoje vesmíru dosáhla za posledních 20 let neuvěřitelného pokroku díky záplavě nových pozorování a teoretickým průlomů. Například inflační scénář velmi ranné fáze vývoje vesmíru vedl k řešení některých hlubokých záhad standardní kosmologie velkého třesku. Předpověděl určité vlastnosti geometrie vesmíru a spektra kosmického mikrovlnného pozadí, které byly potvrzeny nedávnými pozorováními.

Přes své velké úspěchy inflační scénář obsahuje některé hluboké koncepční problémy, které znemožňují zařadit inflační scénář mezi standardní fyzikální teorie. Například inflační teorie se skalárním polem je ve stejném smyslu nekompletní jako byla standardní kosmologie velkého třesku: v kontextu inflační kosmologie je počáteční singularita nepochybným faktem a proto zde nelze konzistentně formulovat problém počátečních podmínek. Vážnějším problémem inflační teorie je fakt, že úspěšná předpověď vlastností kosmického mikrovlnného pozadí v současných inflačních modelech (s exponenciálním rozpínáním prostoru, které je ovládáno potenciální energií skalárního hmotného pole) souvisí s extrapolací této fyzikální teorie do situace, kde její základy (zejména klasická obecná teorie relativity a slabě vázaná kvantová teorie pole) ztrácejí svoji platnost. Achillovou patou inflační kosmologie je problém kosmologické konstanty. Jak víme, že dosud neznámý mechanismus, který dnes ruší energii vakua, tuto energii nerušil v době, kdy byla potřebná pro průběh inflace? Kromě těchto a dalších koncepčních problémů dosud neexistuje přesvědčivá realizace inflačního mechanismu v kontextu běžných modelů částicové fyziky, která by vycházela z kvantové teorie pole.

Současná pozorování jsou také výzvou některým předpokladům našich současných kosmologických modelů. Pozorování například naznačují, že ve vesmíru existuje temná hmota, která představuje významnou část hustoty energie, ale tato hmota nevytváří shluky. Nedávná měření a numerické simulace odhalují vážné rozpory mezi předpokládanou a pozorovanou strukturou galaktických hal. Měření naznačují, že temná hmota nemusí být chladná, jak se původně předpokládalo.

Autor článku [X1] se domnívá, že nejlepším kandidátem na sjednocenou teorii všech silových interakcí a na kvantovou teorii prostoročasu a hmoty je teorie superstrun (nebo M-teorie). Tato teorie se snaží vyřešit rozpory mezi kvantovou teorií pole a obecnou teorií relativity. Proto by mohla vyřešit také otevřené problémy kosmologie počátečních fází vývoje vesmíru. Pokud teorie superstrun přijme tuto velkou výzvu, získá nezbytný důležitý kontakt s experimentálními fakty a nebude již ostře kritizována za to, že je spíše čistou matematikou než fyzikální vědou. Úspěšné určení entropie extrémní černé díry v kontextu teorie superstrun je prvním velkým úspěchem spojení této teorie a kosmologie.

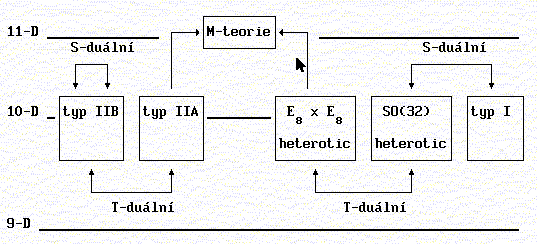
Až donedávna neexistovalo příliš prací, které by nějak teorii superstrun a kosmologii spojovaly. Avšak již od konce 80. let 20. století bylo jasné, že teorie superstrun bude zřejmě schopna vyřešit některé problémy standardní kosmologie. Například v rámci poruchové teorie superstrun byl využit předpoklad, že všechny prostorové dimenze jsou kompaktifikovány na prstenec. Strunová T-dualita dává do souvislosti teorii, kompaktifikovanou na kružnici (nebo prstenec) poloměru R, s jinou teorií, která je kompaktifikována na kružnici (prstenec) poloměru 1/R. Pokud v jedné teorii je dimenze svinuta do malého poloměru, pak ve druhé teorii je rozvinuta do velkého poloměru, ale obě teorie popisují stejnou fyzikální teorii. Důsledkem této T-duality tedy je, že fyzikální teorie ve velmi malých měřítcích je ekvivalentní fyzikální teorii ve velmi velkých měřítcích, což by mohlo vést k eliminaci prostoročasových singularit. Jednotlivé konzistentní teorie superstrun navzájem souvisejí prostřednictvím dualit, jak naznačuje následující obrázek.

Superstruny mají v kompaktifikovaném prostoru jednu důležitou vlastnost. Mohou se navíjet kolem kompaktifikované dimenze, což se projevuje navíjecími módy v hmotnostním spektru. Uzavřená struna se může navinout kolem periodické dimenze celočíselněkrát. Podobně jako v Kaluzově-Kleinově případě navíjecí módy definují momenty hybnosti p = w.R (w = 0, 1, 2, ...). Závislost momentu hybnosti na poloměru kompaktní dimenze je jiná, než ve výše diskutovaném případě. Pokud se kompaktní dimenze zmenšuje, mezery mezi možnými hodnotami momentu hybnosti se také zmenšují.

Strunové navíjecí módy mohou přímo souviset s mechanismem, který umožnil, aby se pouze tři prostorové dimenze zvětšily. Toto dynamické řešení umožňuje překonat problém, že teorie superstrun je konzistentní pouze v devíti prostorových dimenzích (nebo v deseti dimenzích v rámci M-teorie). Teorie superstrun by tak mohly opustit říši čisté matematiky a filozofie a stát se pozorováním falzifikovatelnou teorií.

V polovině 90. let 20. století došlo ve teoriích superstrun ke "druhé revoluci" objevem D-brán. Superstruny mohou mít různé druhy okrajových podmínek. Uzavřené superstruny mohou mít např. periodické okrajové podmínky (uzavřené superstruny přecházejí sami na sebe). Otevřené superstruny mohou mít dva druhy okrajových podmínek, Neumannovy a Dirichletovy okrajové podmínky. Při Neumannových okrajových podmínkách se mohou konce otevřených strun volně pohybovat, ale nedochází ke změně momentu. Při Dirichletových okrajových podmínkách jsou konce otevřených strun upevněny a mohou se pohybovat pouze po určité varietě. Tato varieta se nazývá D-brána nebo D_p-brána (kde p je celé číslo a označuje počet prostorových rozměrů variety).

D-brány mohou mít rozměry od -1 do počtu prostorových rozměrů našeho prostoročasu. Např. Superstruny existují v 10-rozměrném prostoročasu, který má 9 prostorových a jednu časovou dimenzi. Proto je D₉-brána horní limitou teorie superstrun. Pokud je koncový bod superstruny upevněn na varietě, která vyplňuje celý prostor, pak se může pohybovat kdekoliv v tomto prostoru beze změny momentu a fakticky jde o Neumannovu okrajovou podmínku.

Případ p = -1 popisuje situaci, kdy jsou všechny prostorové a časová dimenze pevné. Tento případ se označuje D-instanton. Pokud je p = 0, pak jsou všechny prostorové dimenze pevné a koncový bod struny existuje jako obyčejný bod v prostoročase. Tato D₀-brána se také označuje jako D-částice. D-brány jsou sami o sobě dynamickými objekty, které mají své fluktuace a mohou se pohybovat.

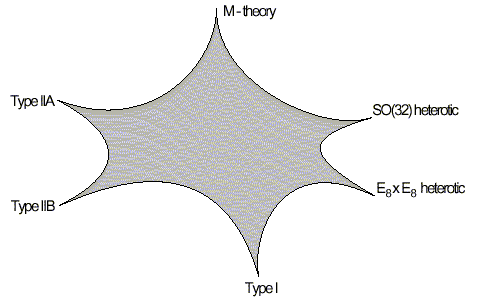
S objevem D-brán bylo zřejmé, že existuje mnohem více fundamentálních stupňů volnosti, než jsou pouze superstruny. Mezi pěti konzistentními teoriemi superstrun byly objeveny duality, které naznačují, že by mohla existovat obecnější teorie, dnes označovaná jako M-teorie. Různé teorie superstrun (včetně 11- rozměrné supergravitace) odpovídají jen různým částem M-teorie, jak naznačuje následující obrázek.

Dalším důležitým nástrojem se stala AdS-CFT korespondence, která dává do souvislosti klasickou gravitaci na anti-de Sitterově pozadí s konformní teorií pole na jeho hranici. Nedávno se pozornost soustředila na scénáře bránového světa (brane world), které jsou kombinací předchozích myšlenek, kdy hmotná pole našeho vesmíru jsou upevněna na jisté 3-bráně a gravitace existuje ve vícerozměrném objemu. Obecně prostorové dimenze procházející bránami musí být řádově velmi malé, aby nedošlo k příliš velkým odchylkám od Newtonova gravitačního zákona. Objevila se také zajímavá myšlenka, které původně nesouvisela s teorií superstrun. Tato myšlenka předpokládala, že kromě tří prostorových dimenzí a jedné časové dimenze ještě další dvě dimenze mají makroskopickou velikost (řádově 1 mm). Protože 4- rozměrná efektivní gravitační konstanta souvisí s fundamentální vícerozměrnou gravitační konstantou prostřednictvím velikosti dodatečných rozměrů, lze fundamentální gravitační konstantu redukovat v TeV řádech energie za předpokladu, že dvě dodatečné dimenze mají velikost řádově jednoho milimetru. Tato myšlenka by mohla vyřešit problém hierarchie hmotností elementárních částic. Pokud gravitace zůstává upevněna na určitou bránu, mohou být některé dodatečné dimenze velkých rozměrů (dokonce nekonečně velké).

Na druhé straně dosud neexistuje žádná neporuchová formulace M-teorie. Dokonce nevíme, kolik fundamentálních stupňů volnosti může tato teorie mít. Jednou ze slibných teorií souvisejících s M-teorií je kvantově mechanický maticový model. Některé jeho nekomutativní vlastnosti by mohly souviset s nekomutativitou prostoročasových souřadnic v mikroskopickém měřítku. Další vážný problém souvisí s tím, že modulační prostor vakuových stavů odpovídající určité teorii superstrun je velmi velký. Přitom většina předpovědí částicové fyziky a kosmologie závisí na výběru modulace vakuového stavu. Proto klíčovým úkolem superstrunové kosmologie je nalézt vakuový stav, který odpovídá našemu vesmíru. Protože modulace vakuových stavů odpovídají nehmotným polím, proč nepozorujeme nehmotné částice, které by odpovídaly těmto vakuovým stavům?

Přes všechny problémy superstrunové kosmologie nabídla slibná řešení řady otázek. Jednou z takových otázek je, zda tato kosmologie bude schopna zodpovědět, jak dlouho muselo trvat inflační rozpínání vesmíru. Pokud superstrunová kosmologie takovou odpověď nabídne, bude záležet na pozorování, aby rozhodlo mezi superstrunovými inflačními modely a inflačním modelem se skalárním polem. Toto rozhodnutí bude nepochybně souviset s pochopením hustotních fluktuací a anisotropie kosmického mikrovlnného pozadí. Na druhé straně teorie superstrun nemusí přispět k problémům inflačního scénáře, ale může přispět k řešení problémů standardní kosmologie velkého třesku, jako je problém horizontu a plochosti vesmíru. Tuto možnost nabízí superstrunová kosmologie zabývající se obdobím před velkým třeskem. Tato kosmologie vychází z dilatonové gravitace jako efektivní teorie v nízkých energiích, která je konzistentní se symetriemi teorie superstrun. Radikálnější variantou inflace, která řeší problém homogenity a plochosti vesmíru, je scénář s měnící se rychlostí světla, kdy rychlost světla v počátečních fázích vývoje vesmíru byla o mnoho řádů vyšší, než je její současná hodnota.

Přímým pozorováním lze ověřit také problém temné hmoty, jehož řešení superstrunová kosmologie nabízí. Protože superstrunová kosmologie vede k velkému počtu skalárních polí, nabízí se vysvětlení původu temné hmoty pomocí potenciálu těchto polí. S tím souvisí problém pozorované malé hodnoty kosmologické konstanty. Konečně, dokonce bez znalosti přesné modulace vakuového stavu, teorie superstrun lze ověřit, zda teorie superstrun vskutku řeší problém singularit standardního kosmologického modelu.

Zájem o superstrunovou kosmologii roste. Autor článku [X1] uvádí, že na přelomu července a srpna 2000 proběhlo pracovní setkání na Univerzitě Britské Kolumbie ve Vancouveru, která se věnovalo superstrunové kosmologii. Toto pracovní setkání sponzorovaly Pacifický ústav matematických věd (the Pacific Institute for Mathematical Sciences), Kanadský ústav pokročilého výzkumu (the Canadian Institute for Advanced Research) a APCTP. Mezi pozvanými vědci byli B. Greene (Columbia Univ.), N. Kaloper (Stanford), L. Kofman (CITA, Univ. of Toronto), D. Lowe (Brown Univ.), B. Ovrut (Univ. of Pennsylvania), S. Ramgoolam (Brown Univ.), S. Sin (Hanyang Univ.), D. Son (Columbia Univ.), P. Steinhardt (Princeton Univ.), H. Verlinde (Princeton Univ.), G. Veneziano (CERN) a A. Zhitnitsky (UBC). Autor článku [X1] uvádí, že setkání se zabývalo dalšími směry vývoje superstrunové kosmologie.

Jedním ze slibných směrů superstrunové kosmologie je kosmologie období před velkým třeskem. Teoretikové očekávají, že mezi superstrunovou kosmologií a inflační kosmologií se skalárním polem budou důležité rozdíly. Kosmologie období před velkým třeskem je popisem fyziky nízkých energií, která bere v úvahu všechny módy nízkých energií v teorii superstrun, tedy nejen graviton, ale také dilaton a antisymetrické tensorové pole (které však pro dynamiku pozadí na úrovni homogenních pohybových rovnic nehraje důležitou roli). Symetrie a pohybové rovnice pro dilatonovou gravitaci vedou ke scénáři, kdy vesmír svoji existenci začíná ve stavu blízkém poruchovému strunovému vakuu, prochází dilatonovou fází kontrakce, během níž Hubbleův poloměr H^-1(t) (H je rychlost expanze, t je čas) se smršťuje rychleji než fyzikální délka spoluměnících se měřítek. Tím se současně řeší problém horizontu ve standardní kosmologii a problém mechanismu vzniku velkoobjemových struktur jako jsou galaxie. Kvantově mechanické fluktuace, které existují během fáze smršťování v sub-Hubbleově měřítku, zamrzají, když se Hubbleův poloměr zmenší pod velikost vlnových délek těchto fluktuací. Naopak se tyto kvantové fluktuace super-adiabaticky zesilují, když je jejich vlnová délka větší než Hubbleův poloměr. Tím kvantové fluktuace vstupují znovu do hry v pozdějších fázích vývoje vesmíru jako klasické fluktuace hustoty. Když se vesmír smršťuje, jeho křivost roste.

Existuje také možnost, jíž nelze popsat pomocí rovnic dilatonové gravitace. Vesmír během své fáze kontrakce fázově přechází do rozpínající se Friedmanovy kosmologie prostřednictvím určité duální transformace. Je třeba poznamenat, že kosmologie období před velkým třeskem vývoj pozadí a spektrum indukovaných fluktuací popisuje jiným způsobem než inflační modely se skalárním polem. Fluktuace hustoty, vycházející z dilatonového řešení, nejsou škálově invariantní. Ve velkých měřítcích jsou naprosto zanedbatelné. Ostatní pole v období před velkým třeskem (jako je axion) však vytvářejí fluktuace, které mohou být škálově invariantní. Protože tyto fluktuace začínají jako fluktuace isokřivosti, mohou vést k odlišným předpovědím pro pozorování, jako je anisotropie spektra kosmologického mikrovlnného pozadí, než jsou předpovědi skalárně metrických fluktuací inflační kosmologie.

Vidíme tedy, že superstrunová kosmologie vede k předpovědím, které jsou dostatečně odlišné od standardní inflační kosmologie. Proto bude možno obě teorie falzifikovat pozorováním.

Kosmologie období před velkým třeskem se potýká také s problémem "hladkého ukončení". V kontextu pohybových rovnic dilatonové gravitace období smršťování končí v singularitě a období rozpínání ze stejné singularity vychází. Protože singularita se objevuje v okamžiku vysoké křivosti prostoročasu, je zřejmé, že akce efektivní dilatonové gravitace není správným popisem superstrunové fyziky v blízkosti singularity. Další výzvou pro superstrunovou kosmologii tedy je zjistit, zda teorie superstrun je schopna nalézt vhodný mechanismus hladkého přechodu z období smršťování do období rozpínání s pevnou hodnotou dilatonu. Přestože již existuje několik pokusů řešit problém "hladkého ukončení" za hranicemi platnosti dilatonové gravitace, žádný z nich dosud nevedl k zásadnějším výsledkům. Důležitým otevřeným problémem superstrunové kosmologie je vývoj skutečně strunové neporuchové verze scénáře vývoje vesmíru před velkým třeskem nebo modifikace původního inflačního scénáře tak, aby vedl ke skutečně superstrunovému kosmologickému modelu.

Další slibný směr vývoje superstrunové kosmologie vychází z teorie P. Hořavy a Edwarda Wittena, která se někdy nazývá kosmologie založená na heterotické M-teorii. Tato teorie vychází z kompaktifikace 11-rozměrné supergravitace na orbivarietu (orbifold) S¹/Z₂. Jako obvykle se předpokládá kompaktifikace šesti rozměrů na zvláštní typ Calabiovy-Yauovy variety a existuje zde množina E₈ kalibračních supermultipletů na každé ploše orbivariety. Důvodem kompaktifikace na orbivarietu je umožnit existenci chirálních fermionů. Výsledná teorie je duální k E₈ x E₈ heterotické teorii se silnou vazbou. Podle této teorie v jisté fázi vývoje musela být dynamika vesmíru pětirozměrná. Nedávno se ukázalo, že dynamika zmíněné teorie je zcela netriviální a může vést k velkému zájmu ze strany některých kosmologů.

Poněkud jiný směr vývoje superstrunové kosmologie vychází z předpokladů analogických běžným východiskům kosmologie velkého třesku. Předpokládá se, že vývoj vesmíru začíná v Planckově měřítku a vesmír prochází horkou fází, v níž jsou excitovány všechny stupně volnosti. Je přirozené zobecnit tento výchozí bod na superstrunovou kosmologii a předpokládat, že vesmír začal svoji existenci s prostorovými dimenzemi strunových měřítek a že všechny fundamentální stupně volnosti byly excitovány podle svého termálního rozdělení. Proto také strunové a bránové navíjecí módy byly vysoce excitovány. Tato hypotéza se někdy nazývá hypotézou "bránového plynu". Všechny prostorové dimenze jsou na počátku kompaktifikovány. Otázkou kosmologie již není, proč jsou určité dimenze kompaktifikovány, ale naopak proč se pevný počet dimenzí dekompaktifikoval (ve smyslu, že jejich poloměr se stal větším než je současný Hubbleův poloměr vesmíru). V poslední době bylo dosaženo jistých zajímavých výsledků. Za předpokladu, že všechny prostorové dimenze jsou kompaktifikovány na prstenec, se ukazuje, že počáteční fázi vývoje ovládaly vícerozměrné brány a pozdější fázi měly klíčový význam fundamentální struny. Superstrunová kosmologie studuje mechanismus, který umožnil, že pouze tři prostorové dimenze byly dekompaktifikovány do velkých měřítek. Dualita navíc zajišťuje, že se neobjevují žádné singularity.

V současné době zřejmě největší pozornost přitahuje skupina scénářů "bránového světa". Výchozím bodem těchto scénářů je předpoklad, že všechna hmotná pole jsou upoutána na 3-bránu vloženou do vícerozměrného (obvykle pětirozměrného) prostoročasu. Přitom lze gravitaci připoutat na jednu z těchto bran tím, že čtyřrozměrná metrika závisí na páté souřadnici. V řadě případů tato metrika je anti-de Sitterova na základě korespondence AdS-CFT, která dává do souvislosti klasickou gravitaci na anti-de Sitterově pozadí s konformní teorií pole na jeho hranici. Bohužel může existovat neomezený počet tohoto základního scénáře. Proto naléhavým úkolem superstrunové kosmologie je odvodit základní pravidla, které scénáře "bránového světa" musí dodržet, pokud mají vycházet z teorie superstrun. Zatím existují nezodpovězené otázky.

Podle autora článku [X1] by konečný kosmologický model měl vycházet z neporuchové formulace M-teorie. Pokud dnes vyjdeme z maticové teorie, zdá se, že výsledná prostoročasová teorie bude ve strunovém měřítku nekomutativní. Omezením dnešní maticové teorie je fakt, že je definována pouze v souřadnicích světelného kuželu.

Základním problémem všech směrů superstrunové kosmologie je modulační problém. Co zmrazilo hodnotu dilatonu a co nastavilo měřítko dodatečných rozměrů? Obvykle předpokládáme, že v pozadí stojí nějaká neporuchová fyzika. Pokud nějaký efektivní potenciál zajišťuje požadovaný mechanismus, proč hodnota tohoto potenciálu v jeho minimu nevedla k jiné kosmologické konstantě? Zdá se, že problém modulace a problém kosmologické konstanty spolu nějak souvisejí.

Superstrunová kosmologie je ještě ve svých dětských letech. Přestože již existuje řada zajímavých směrů, které spojují teorii superstrun a kosmologii, drtivá většina z nich trpí tím, že dosud nemáme neporuchovou formulaci teorie superstrun.

Literatura a odkazy:

[X1] Robert H. Brandenberger: The Promise of String Cosmology. March 20, 2001. Department of Physics, Brown University, Providence, RI 02912, USA.

[F1] Teorie superstrun.Historie teorie superstrun. Principy teorií superstrun. Strunová dualita. Teorie superstrun a záhada ztráty informace. Nedávné výsledky teorií superstrun. Aplikace teorie superstrun v kalibračních teoriích. Kalibrační teorie a membránové teorie. Závěr.