Fyzikální paradoxy jsou logické úvahy vedoucí k překvapujícím nebo nesprávným závěrům. Jejich fyzikální argumenty často vedou k určitým nefyzikálním důsledkům.

Fyzikální paradoxy zaujímají v historii vědy zvláštní místo, protože často vedou k vědeckým přelomům a k novému pohledu na svět kolem nás. Nové přístupy při pokusu řešit paradoxy mohou vést k intelektuálním zlomům v myšlení.

Nejstarší známé logické paradoxy sestavil řecký filozof Zenón z ostrova Elea v jižní Itálii. Nejznámějším paradoxem je paradox Achillea a želvy. Achilles běží za želvou. Za dobu, kterou potřebuje k dosažení místa, na kterém želva stála v okamžiku jeho startu želva postoupí o určitou vzdálenost. Než tuto vzdálenost Achilles překoná, želva znovu postoupí o určitou malou vzdálenost. Achilles proto želvu nikdy nedostihne. Matematik dr. Jiří Mrázek ve své knize "Taje matematiky" vysvětluje, že Zenón použil chybného chápání pojmu nekonečna. Součet nekonečně mnoha veličin nemusí být nekonečný, což zajisté věděl i Zenón, ale jeho snahou bylo poukázat na značné potíže v učení pythagorejců. [1]

Naproti tomu Whitrow po pečlivé analýze dospěl k názoru, že buď je nutné odmítnout pojem "změny" a čas tak získá prostorové vlastnosti, anebo čas je podobně jako prostor dělitelný na nekonečně malé části. [2] Proti tomuto druhému názoru ale zřejmě stojí poznatky kvantové teorie. Kvantové efekty geometrie prostoročasu způsobují, že evoluci vesmíru lze sledovat nikoliv do času t = 0, ale pouze do Planckova času 10^-43 s po velkém třesku. V časech kratších ztrácí prostoročas vlivem kvantových fluktuací své obvyklé lokální topologické vlastnosti, takže zde nelze sledovat kauzalitu příčin a důsledků. Proto ani kratší časový interval, než je Planckův čas, nemá zřejmě fyzikální smysl. [3], [4]

Jiným známým paradoxem klasické fyziky bylo Aristotelovo tvrzení, podle něhož těžší tělesa padají rychleji než tělesa lehčí. Galileo Galilei ale vytvořil myšlenkový paradox. Uvažujme dvě stejně hmotné zlaté mince. Podle Aristotela budou padat na zem stejnou rychlostí. Nyní si ale představme, že tyto mince jsou spojeny velmi lehkým vláknem. Podle Aristotela tvoří jedno těleso s dvojnásobnou hmotností, takže musí padat dvakrát rychleji. Ale proč, když jsou spojeny jen tenkým vláknem? Galileo Galiei tento paradox správně analyzoval, a dospěl k závěru, že se Aristoteles zmýlil a všechna tělesa (pokud zanedbáme odpor vzduchu) musí padat stejnou rychlostí bez ohledu na svou hmotnost. Tato analýza se později stala základem moderní dynamiky, na které o století později stavěl Isaac Newton, když objevil své zákony pohybu.

Dalším dobře známým paradoxem je Olbersův paradox. Německý astronom Heinrich Olbers se zamýšlel nad tím, proč noční obloha není stejnoměrně jasná jako povrch Slunce? Pokud vesmír obsahuje nekonečně mnoho hvězd, měli bychom v každém směru pozorovat záření z některé hvězdy. Jestliže by Slunce bylo dvojnásobně vzdáleno než je nyní, přijímaly bychom 1/4 původního množství fotonů, ale současně by úhlový průměr Slunce klesl na 1/4 původního průměru. Intenzita záření v dané ploše tedy zůstává konstantní. Pokud předpokládáme nekonečně mnoho hvězd ve vesmíru, každý prostorový úhel oblohy bude obsahovat alespoň jednu hvězdu a proto celá obloha by měla zářit jako povrch Slunce. Tuto skutečnost bychom pak mohli vyjádřit tak, že žijeme uvnitř dutiny absolutně černého tělesa s termodynamickou teplotou asi 6 tisíc stupňů Kelvina. [I1]

Řešení tohoto paradoxu přišlo až ve 20. století, kdy Edwin Hubble v roce 1929 objevil kosmologické rozpínání vesmíru. Záření vzdálených hvězd a galaxií se vlivem Dopplerova jevu posouvá k červené části spektra.

Albert Einstein koncem 19. století nalezl jiný paradox. Podle Maxwellovy teorie elektromagnetického pole je světelná vlna kombinací elektrického pole a magnetického pole, která jsou vzájemně kolmá a při pohybu prostorem oscilují mezi kladnými a zápornými hodnotami. Pokud se pozorovatel pohybuje rychlostí světla vedle vlny, žádnou oscilaci nepozoruje, což ale porušuje zákony fyziky. Zákony, které platí v jedné vztažné soustavě, přestávají platit v jiné vztažné soustavě. Tento paradox Einsteina přivedl k vytvoření speciální teorie relativity, v níž zákony fyziky platí ve všech inerciálních vztažných soustavách.
 

Ve 20. letech 20. století vznikla kvantová mechanika, která vysvětlovala mikroskopické jevy. V roce 1935 Albert Einstein, Boris Podolsky a Nathan Rosen zformulovali myšlenkový experiment, dnes známý jako EPR paradox, který je dosud předmětem debat. Einstein v tomto paradoxu kritizoval princip nelokalizace, podle něhož některé kvantové vztahy jsou realizovány tak, jako by se informace šířila rychlostí vyšší než je rychlost světla ve vakuu. EPR paradox vedl k řadě interpretací kvantové mechaniky, které se snažily tento a další paradoxy kvantové teorie odstranit. [I2]

V roce 1960 John Bell ukázal, že dvojice korelovaných částic, které nejprve jsou v kontaktu a pak se od sebe vzdálí na libovolnou vzdálenost, budou vykazovat vzájemně korelovaná náhodná chování, která nelze vysvětlit klasickou statistikou. Experimenty prováděné s fotony a s jinými částicemi opakovaně potvrzují tuto korelaci, což lze považovat za silný důkaz platnosti kvantové mechaniky. Důležitým faktem EPR korelace je skutečnost, že nepřenáší měřitelnou a řiditelnou informaci, tedy ji nelze použít k přenosu dat. Zdálo se, že tedy slouží pouze k důkazu kvantové mechaniky. Ale v 90. letech 20. století bylo experimenty opakovaně prokázáno, že může sloužit ke kvantové teleportaci, kdy se přenáší ta část informace o objektu, která nebyla snímána a přenesena konvenčními metodami. [I2]

V roce 1993 mezinárodní skupina šesti vědců, z nichž jedním byl pracovník IBM Charles H. Bennet, ukázala, jak proces kvantové teleportace lze experimentálně ověřit. [5]

Ještě donedávna se vědci o jev teleportace vážně nezajímali, protože se myslelo, že porušuje Heisenbergův princip neurčitosti kvantové mechaniky, který zamezuje získání úplné informace o atomu nebo jiném objektu. Podle principu neurčitosti čím více se získá informací o objektu, tím více se objekt narušuje, až se původní stav objektu zcela změní, aniž se podaří o objektu získat kompletní informaci, z níž by se pak získala přesná kopie. Zdálo se, že jde o velmi silný argument proti jevu teleportace: nelze sejmout dostatečnou informaci o objektu, aby bylo možno vytvořit jeho přesnou kopii. Tým Charlese H. Benneta [5] však nalezl způsob, jak tento logický argument obejít. Použili k tomu EPR paradox. Stručně řečeno, nalezli metodu, jak sejmout část informace z objektu A, který má být teleportován, zatímco zbytek informace se přenese pomocí objektu C prostřednictvím efektu EPR, aniž tento objekt byl v kontaktu s objektem A. Později je možné takto uchovanou informaci použít k rekonstrukci objektu A, který však již není ve svém původním stavu, neboť tento stav byl narušen snímáním informace. Proto tato metoda může sloužit k teleportaci, ale nikoliv k replikaci objektu A.

Kvantovou teleportaci poprvé experimentálně demonstrovali fyzikové z University v Innsbrucku (Anton Zeilinger, Dik Bouwmeester). Princip kvantové teleportace, který byl navržen v roce 1993 Charlesem H. Bennettem z IBM, umožňuje fyzikům vzít foton (nebo jinou částici kvantových rozměrů, jako je atom) a přenést jeho kvantové vlastnosti (jako je polarizace) na jiný foton, a to dokonce i v případě, že oba fotony jsou na různých koncích galaxie. [I3]

Další verzi kvantové teleportace publikovali vědci z Itálie a Velké Británie (Francesco DeMartini, Univerzita v Římě). Podobně jako v experimentu v Innsbrucku, byla použita dvojice kvantově propletených (vázaných) fotonů. Zatímco v experimentu z Innsbrucku se teleportuje hodnota polarizace třetího fotonu (přenášená "zpráva") jedním z vázaných fotonů, v experimentu v Římě byl jeden z vázaných fotonů uveden do speciálního stavu polarizace a tento stav se přenesl na druhý vázaný foton. Na rozdíl od experimentu v Innsbrucku, který byl úspěšný pouze v 25 procentech, toto schéma má úspěšnost 100 procent, pokud se použijí správné transformace na druhý foton. (D. Boschi et al., článek v Physical Review Letters). V jiné teoretické práci Sam Braunstein z University of Wales (Bangor) a Jeff Kimble z Caltechu navrhují experimentální metodu pro rozšíření kvantové teleportace z přenosu diskrétních veličin, jako je polarizace, na přenos spojitých veličin, jako je amplituda elektrického pole spojeného se světelným vlněním. (Braunstein et al., Phys. Rev. Lett., 26 January 1998.) [I3]
 

V roce 1987 A. Datta, D. Home a A. Raychaudhuri objevili nový paradox kvantové mechaniky, označený podle Univerzity v Kalkatě jako Kalkatský paradox. Paradox využíval zvláštnosti neutrálních mesonů K (kaonů) jako důkaz komunikace nadsvětelnou rychlostí. Nadsvětelnou komunikaci většina fyziků odmítá, protože představuje porušení nejen speciální teorie relativity, ale také principu kauzality jevů.

Mesony jsou částice fyziky vysokých energií. Jejich hmotnost se obvykle pohybuje mezi hmotností elektronu a protonu a jejich délka života je jen několik miliardtin sekundy.

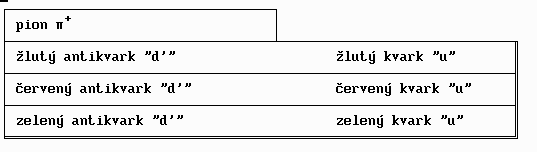
Mesony jsou složeny z páru kvark a antikvark (viz pozn. 1). Kvantová veličina označovaná jako barva kvarku se mění spojitě v čase tak, aby meson zůstal bezbarvý. Například kladný meson pí (pion) je složen následujícím způsobem:

Neutrální kaon je složen následujícím způsobem:

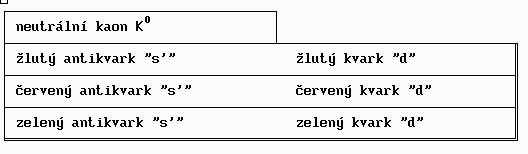
Neutrální antikaon je složen z kvarku "s" a antikvarku "d". Neutrální kaon a neutrální antikaon mají nulový elektrický náboj a nulový spin. Obě částice mají stejnou hmotnost, rovnou zhruba polovině hmotnosti protonu. Z hlediska pozorování jsou tyto kaony nerozlišitelné. Pokud jsou dva kvantové stavy nerozlišitelné, mohou se vzájemně superponovat do nových stavů, které jsou také nerozlišitelné. V případě neutrálních kaonů se kaony a antikaony kombinují dvěma různými způsoby. Vytvářejí jednak částici K⁰_S (K-short), která se rozpadá na dva nebo tři piony za dobu kolem 10^-10 sekundy a jednak částici K⁰_L (K-long), která se rozpadá 581-krát pomaleji. Kaon K⁰_L porušuje invarianci CP (invarianci vůči změně náboje a vůči zrcadlení). [6]

Představme si svazek neutrálních kaonů. Obsahuje dvě složky, K⁰_S a K⁰_L, z nichž první se asi za 10^-10 rozpadne na dva piony. Druhá složka, která obsahuje neutrální kaony a antikaony, existuje ještě asi 50 ns a pak se rozpadne na tři piony. Během této doby může dojít ke srážce s protonem nebo atomovým jádrem. Tím se obě složky obnoví v původním poměru a následuje rozpad složky K⁰_S a poté znovu složky K⁰_L. Tento jev se nazývá regenerace krátkodobé složky.

Je možný i velice vzácný rozpad složky K⁰_L na dva piony. Objevili jej Val L. Fitch a James W. Cronin v roce 1964 a je důkazem toho, že slabá interakce skutečně porušuje invarianci vůči transformaci CP. Dnes tento kvantový jev nemá výrazný význam, ale při vzniku vesmíru ovlivnil fundamentální asymetrii mezi hmotou a antihmotou a tím zřejmě podmínil naši vlastní existenci. [6]

Kalkatský paradox používal proces, k němuž dochází, když se kaon K⁰_L pohybuje jedním směrem a kaon K⁰_S opačným směrem. Autoři ve své práci dokazovali, že detektor antikaonů umístěný v jednom směru zaregistruje rozdílný počet částic, pokud ve druhém směru je umístěna měděná deska. Pozorovatel by tak mohl pomocí měděné desky v jednom směru přenášet zprávu pozorovateli ve druhém směru nadsvětelnou rychlostí, což je paradoxní.

V roce 1996 se prokázalo, že Kalkatský paradox vznikl chybným kvantově mechanickým výpočtem a šlo tedy o jeden z omylů ve vědě.
 

John Archibald Wheeler ve svých esejích o kvantové mechanice "Quantum Theory and Measurement" [7] uvádí, že kvantová mechanika zbavila fyziku řady představ a předsudků.

Kvantová mechanika zbořila představu fyziků, že fyzikální veličiny, jako je poloha nebo hybnost, jsou dány někde mimo, nezávisle na pozorování. Informace o kvantovém světě získáváme postupně, krok za krokem, podle toho, jaké experimenty provádíme. Pokud bychom měřili jiné fyzikální veličiny nebo je měřili v jiném pořadí, můžeme dospět k jiným závěrům. Při experimentech ovlivňujeme, co se s měřeným systémem stane. Nevíme přesně, jaké výsledky měřením získáme. Přitom pozorování kvantových systémů je vždy konzistentní.

V reálném světě kvantové fyziky žádný elementární jev není jevem, dokud není pozorovaným jevem. Nikde nečekají fyzikální veličiny na to, až provedeme jejich měření. Thomas Mann napsal, že ve skutečnosti jsme to my, kdo způsobuje to, co se jeví. Snad přeháněl, ale nelze popřít, že každý pozorovatel je účastníkem procesu zjevování reality. Je možné, že zatím postrádáme to hlavní, totiž roli kvantových principů v konstrukci vesmíru. [7]

Reference autora článku [X1]:

* Zenónovy paradoxy:
W. V. Quine, Scientific American 206, #4 (April, 1962), pp. 84-96.

* EPR Paradox:
A. Einstein, B. Podolsky, and N. Rosen, Phys. Rev. 47 (1935) 777.

* Kalkatský paradox:
A. Datta, D. Home, and A. Raychaudhuri, Phys. Lett. A 123 (1987) 4.

* Neutrální mesony K:
Robert Adair, Scientific American 258, #2 (February, 1988).
 

Standardní model teorie elementárních částic popisuje hmotové částice (fermiony, poločíselný spin) a částice zprostředkující silové interakce (bosony, celočíselný spin). Model lze shrnout do následujících schémat:

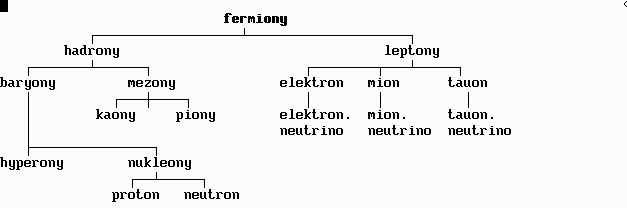
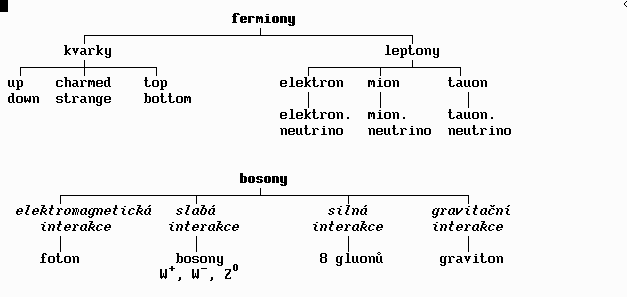
V 60. letech 20. století vyslovili fyzikové Murray Gell-Man a G. Zweig domněnku, že hadrony se skládají ještě z elementárnějších částic, které nazvaly kvarky.

Kvarků je celá řada. Podle kvantové charakteristiky nazvané "vůně" je šest kvarků u, d, s, c, b, t. Toto označení kvarků vychází z anglických slov "up", "down", "strange" (podivný), "charmed" (půvabný), "bottom" (spodní) a "top" (svrchní). Každá "vůně" se přitom vyskytuje ve třech "barvách", což je další kvantová charakteristika, a to červené, zelené a modré.

Pravidlo pro sestavení hadronů říká, že baryon je složen ze tří kvarků, z nichž každý musí mít jinou barvu. Meson se pak skládá z páru kvark a antikvark téže barvy (kvark má barvu, antikvark má antibarvu, proto se celkově meson jeví jako bezbarvý).

Kvarky mají některé podivné vlastnosti. Jejich elektrický náboj představuje buď třetinu nebo dvě třetiny jednotkového náboje. Kvarky "u", "c" a "t" mají náboj +2/3, kvarky "d", "s" a "b" mají náboj -1/3. Antikvarky "u'", "c'" a "t'" mají náboj -2/3 a antikvarky "d'", "s'" a "b'" mají náboj -1/3.

Literatura a odkazy:

[X1] John G. Cramer: Paradoxes and FTL Communication. Analog Science Fiction & Fact Magazine. The Alternate View Column AV-28. September, 1988.

[1] Mrázek, Jiří: Taje matematiky. Vyd. Práce, Praha 1986.

[2] Coveney, Peter; Highfield, Roger: Šíp času. Nakl. Oldag, Ostrava 1995, ISBN: 80-85954-08-7. orig.: The Arrow of Time, WH Allen (Virgin Publishing Ltd.). Great Britain, 1990

[3] Ullmann, Vojtěch: Gravitace, černé díry a fyzika prostoročasu. Československá astronomická společnost ČSAV, pobočka Ostrava, 1986.

[4] Landau, Lev Davidovič - Lifšic, Jevgenij Michajlovič: Kvantová mechanika. Alfa, Bratislava 1982

[5] C.H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres, and W. Wootters, "Teleporting an Unknown Quantum State via Dual Classical and EPR Channels", Phys. Rev. Lett. vol. 70, pp 1895-1899 (1993)

[6] Fischer, Jan: Průhledy do mikrokosmu. Nakl. Mladá fronta, edice Kolumbus, Praha 1986.

[7] Wheeler, John Archibald: Zákon mimo zákon. Úryvky z esejů o kvantové mechanice. Vesmír 5/1998 (roč. 77).
Z knihy "Quantum Theory and Measurement", ed. John Archibald Wheeler, W. H. Zurek, Princeton University, 1983 přeložil Pavel Cejnar

[I1] Item 8.: Olbers' Paradox. Updated 24-Jan 1993 by SIC, original by Scott I. Chase. From: columbus@osf.org Subject: sci.physics Frequently Asked Questions (Part 2/4) Date: 25 Sep 1995 14:55:01 GMT

[I2] Item 30.: The EPR Paradox and Bell's Inequality Principle. Updated 31-Aug 1993 by SIC, original by John Blanton From: columbus@osf.org. Subject: sci.physics Frequently Asked Questions (Part 4/4) Date: 25 Sep 1995 14:55:08 GMT

[I3] From: physnews@aip.org (AIP listserver) Subject: update.356, PHYSICS NEWS UPDATE. The American Institute of Physics Bulletin of Physics News Number 356 January 27, 1998 by Phillip F. Schewe and Ben Stein

[N1] Teorie elementárních částic, 7. 13.4. Mesony. 13.5. Časová inverze. 13.6. Oscilace a regenerace neutrálních kaonů. Natura 6/1995.
 

časopis o přírodě, vědě a civilizaci